Geolocation in Firefox 3.5 and the iPhone

Today the Mozilla group released Firefox 3.5. This release has many new features, but one that really interests me is the inbuilt geolocation service. This release also comes hot on the heels of the iPhone OS3.0 software upgrade that also brings inbuilt geolocation to the mobile safari browser. Why is this exciting? They are both based upon the W3C geolocation specifications. I’ve previously written about geolocating using various browser plugins. This is a messy way of doing it and required a lot of code forking to cover the different possibilities. Now we have a standard way of doing this type of thing.

How do we do it?

Let’s start by creating a call to the browsers in built location service. We need to firstly check that the browser supports location services. If it does, then make a call to try and get our location. If we get a successful location we can display the latitude and longitude. We may also get an error. This may occur if the user decides not to share their location or there is an error in the system.

<script type="text/javascript">
// Check in the browser supports native geolocation and make a call to the geolocation service
function findLocation() {
  if(navigator.geolocation) {
    navigator.geolocation.getCurrentPosition(successCallback,errorCallback);
  } else {
    var displayLocation = document.getElementById("location");
    displayLocation.innerHTML = "Your browser doesn't support geolocation services";
  }
}

// Extract the latitude and longitude from the response
function successCallback(position) {
  var latitude = position.coords.latitude;
  var longitude = position.coords.longitude;
  var displayLocation = document.getElementById("location");
  displayLocation.innerHTML = "latitude: " + latitude + ", longitude:" + longitude;
}

// There was an error
function errorCallback() {
  var displayLocation = document.getElementById("location");
  displayLocation.innerHTML = "Sorry, we couldn't find your location";
}
</script>

We are now able to display our current latitude and longitude – see example 1.

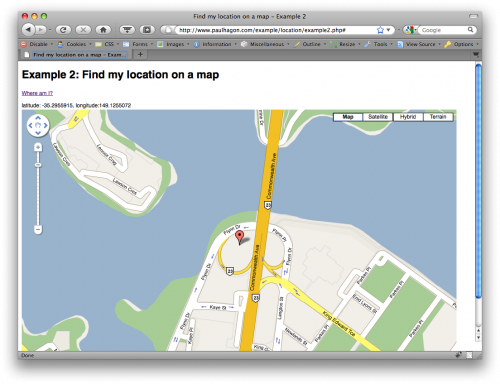
Displaying a map

Now that we have a latitude and longitude it’s much easier to visualise our location if we plot it onto a map.We will keep the same basic code and add some Google Maps script to it.

<script type="text/javascript" src="http://www.google.com/jsapi?key=YOUR_GOOGLE_KEY"></script>
<script type="text/javascript">

// Because we are using a geolocation service we need to make sure sensor=true
google.load("maps", "2", {"other_params":"sensor=true"});

// Check in the browser supports native geolocation and make a call to the geolocation service
function findLocation() {
  if(navigator.geolocation) {
    navigator.geolocation.getCurrentPosition(successCallback,errorCallback);
  } else {
    document.getElementById("location").innerHTML = "Your browser doesn't support geolocation services";
  }
}

// Extract the latitude and longitude from the response and display a map
function successCallback(position) {
  var latitude = position.coords.latitude;
  var longitude = position.coords.longitude;
  document.getElementById("location").innerHTML = "latitude: " + latitude + ", longitude:" + longitude;

 // Display the map
  var map = new GMap2(document.getElementById('map'));

  // Centre the map around the latitude and longitude
  var latlng = new google.maps.LatLng(latitude, longitude);
  var zoom=16;
  map.setCenter(latlng, zoom);

  // display the default controls
  map.setUIToDefault();

  // Add a marker
  var point = new GLatLng(latitude, longitude);
  map.addOverlay(new GMarker(point));
}

// There was an error
function errorCallback() {
  document.getElementById("location").innerHTML = "Sorry, we couldn't find your location";
}
</script>

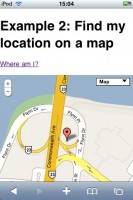
Now it is much easier to determine our location by turning the numbers into something visual and meanignful. Try it out in example 2.

These code samples will work for both Firefox 3.5:

And mobile Safari on iPhones and iPod touches running OS3.0

Now you have the basics of obtaining a latitude and longitude, you can start to use these techniques in your own applications to display locations or items that are relevant to the user in that location.